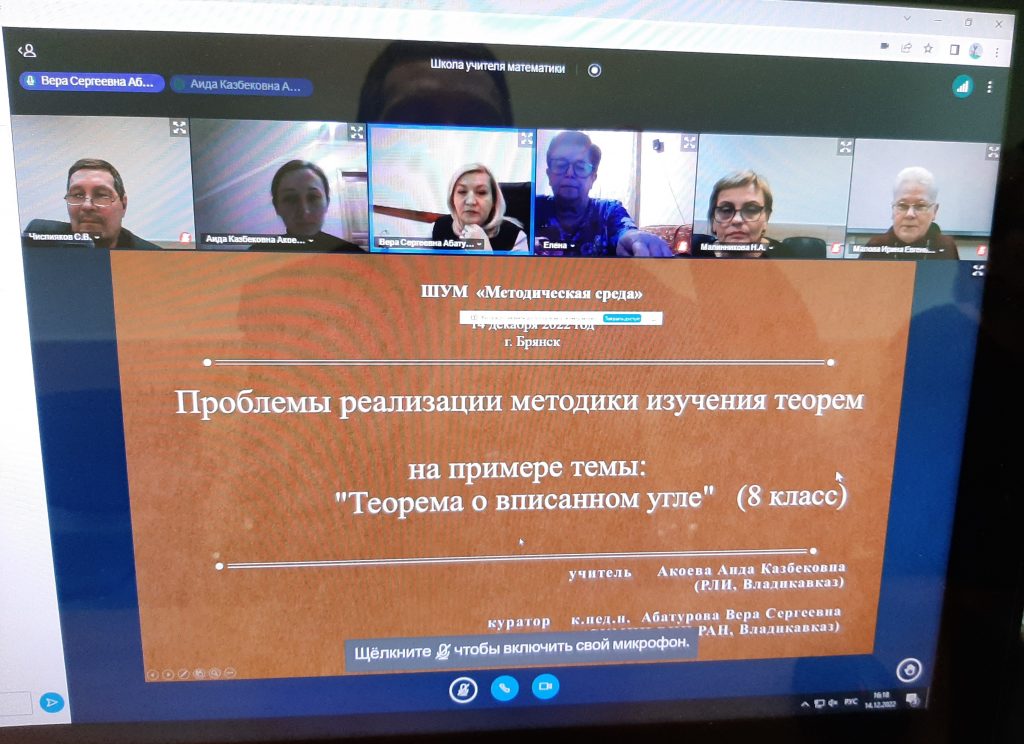
14 декабря 2022 года под руководством профессора кафедры математического анализа, алгебры и геометрии И.Е. Маловой состоялось очередное занятие Школы учителя математики «Методическая среда». В его работе приняли участие преподаватели-кураторы кафедры математического анализа, алгебры и геометрии, учителя математики школ и профессиональных образовательных организаций города Брянска, Беслана, Владикавказа, Алании, обучающиеся магистратуры нашего факультета.
В ходе данного занятия разрешались методические проблемы реализации базовых методик:
– анализ реализации изученных в Школе методических приемов в практике обучения математических дисциплин в школе и вузе;
– раскрытие особенностей методики изучения формул;
– представление способов решения проблемы конструирования урока обучения решению квадратных неравенств;
– выявление методических проблем изучения теорем и разработка путей их решения на примере темы «Центральный и вписанный угол».
В первой части занятия И.Е. Маловой были представлены методические приемы реализуемые в практике обучения математических дисциплин в школе и вузе: использование заданий с пропусками в различных вариантах (разработчик О.П. Охват); использование математических карт (разработчики Ю.А. Еловикова, Н.А. Малинникова, Ф.К. Гусалова); использование систематизирующих таблиц (разработчик Н.А. Малинникова); использование проектного задания по теме «Координатно-векторный метод» (разработчик Ю.А. Еловикова); смысловой анализ рисунка (разработчик А.К. Акоева).
В своем выступлении учитель математики МБОУ СОШ №7 г. Беслана Е.А. Качур раскрыла проблемы конструирования урока обучения решению квадратных неравенств таких как:
– Как организовать этап целеполагания?
– Как организовать введение и усвоение определения квадратного неравенства?
– Как организовать обсуждение идеи способа решения квадратных неравенств с использованием графика квадратичной функции и реализацию идеи на готовых чертежах?
– Как организовать выбор достаточных данных о квадратичной функции для решения квадратного неравенства, введение термина «схематический график»?
– Как организовать введение алгоритма решения квадратного неравенства?
– Как организовать отработку шагов алгоритма решения квадратных неравенств?
– Как организовать подведение итогов урока?
Преподаватель Республиканского лицея искусств г. Владикавказа А.К. Акоева на примере теоремы о вписанном угле раскрыла следующие методические особенности изучения данной темы:
– Как организовать работу по мотивации изучения теоремы?
– Как актуализировать знания, необходимые для введения и доказательства теоремы?
– Как осуществить введение формулировки теоремы конкретно-индуктивным методом?
– Как подвести к идее доказательства теоремы, заключающейся в применении метода полной индукции?
– Какой порядок работы над доказательством выстроить, с учетом “прозрачности” теоремы?
– Как оформить доказательство?
– Каким образом провести усвоение этапов доказательства?
– Каким образом провести непосредственное применение теоремы (первичное закрепление), если в учебнике нет подходящих одношаговых задач?
– Как подвести учащихся к выводу следствий из теоремы о вписанном угле?
– Какого уровня сложности задачи следует рассмотреть с целью закрепления материала?
– Что выбрать для подведения итогов?
Представленные педагогами пути решения проблем вызвали живой интерес и бурное обсуждение у участников и кураторов Школы.
Очередное занятие в Школе состоится 18 января 2022 года. Его темой станут методические проблемы изучения содержательных линий школьного курса математики:
- проблемы конструирования комплексного урока по теме “Логарифмические уравнения”
- проблемы конструирования методики применения алгоритмов в одном задании на примере сложения отрицательных дробей с разными знаменателями и др.
По всем вопросам организации Школы учителя математики необходимо обращаться к научному руководителю Школы профессору кафедры математического анализа, алгебры и геометрии И.Е. Маловой.
Тел.: (4832) 58-93-38, доб.1132, E-mail: mira44@yandex.ru
Для участия в мероприятии необходимо пройти по ссылке https://bbb3.oktcloud.space/b/okt-thi-xy6-iod